How in the hell does anyone f— up so bad they get O(n!²)? 🤯 That’s an insanely quickly-growing graph.
Curious what the purpose of that algorithm would have been. 😅
You have two lists of size n. You want to find the permutations of these two lists that minimizes a certain distance function between them.
Surely you could implement this via a sorting algorithm? If you can prove the distance function is a metric and both lists contains elements from the same space under that metric, isn’t the answer to sort both?
It’s essentially the traveling salesman problem
Let me take a stab at it:
Problem: Given two list of length n, find what elements the two list have in common. (we assume that there are not duplicates within a single list)
Naive solution: For each element in the first list, check if it appears in the second.
Bogo solution: For each permutation of the first list and for each permutation of the second list, check if the first item in each list is the same. If so, report in the output (and make sure to only report it once).
lol, you’d really have to go out of your way in this scenario. First implement a way to get every single permutation of a list, then to ahead with the asinine solution. 😆 But yes, nice one! Your imagination is impressive.
Maybe finding the (n!)²th prime?
I guess, yeah, that’ll do it. Although that’d probably be yet one or a few extra factors involving n.
After all these years I still don’t know how to look at what I’ve coded and tell you a big O math formula for its efficiency.
I don’t even know the words. Like is quadratic worse than polynomial? Or are those two words not legit?
However, I have seen janky performance, used performance tools to examine the problem and then improved things.
I would like to be able to glance at some code and truthfully and accurately and correctly say, “Oh that’s in factorial time,” but it’s just never come up in the blue-collar coding I do, and I can’t afford to spend time on stuff that isn’t necessary.
A quadratic function is just one possible polynomial. They’re also not really related to big-O complexity, where you mostly just care about what the highest exponent is:
O(n^2) vs O(n^3).For most short programs it’s fairly easy to determine the complexity. Just count how many nested loops you have. If there’s no loops, it’s probably
O(1)unless you’re calling other functions that hide the complexity.If there’s one loop that runs N times, it’s
O(n), and if you have a nested loop, it’s likelyO(n^2).You throw out any constant-time portion, so your function’s actual runtime might be the polynomial:
5n^3 + 2n^2 + 6n + 20. But the big-O notation would simply beO(n^3)in that case.I’m simplifying a little, but that’s the overview. I think a lot of people just memorize that certain algorithms have a certain complexity, like binary search being
O(log n)for example.Time complexity is mostly useful in theoretical computer science. In practice it’s rare you need to accurately estimate time complexity. If it’s fast, then it’s fast. If it’s slow, then you should try to make it faster. Often it’s not about optimizing the time complexity to make the code faster.
All you really need to know is:
- Array lookup: O(1)
- Single for loop: O(n)
- Double nested for loop: O(n^2)
- Triple nested for loop: O(n^3)
- Sorting: O(n log n)
There are exceptions, so don’t always follow these rules blindly.
It’s hard to just “accidentally” write code that’s O(n!), so don’t worry about it too much.
lim n->inf t(n) <= O*c, where O is what is inside of big O and c is positive constant.
Basically you can say that time it takes never goes above grapf of some function scaled by constant.
Fun side effect of this is that you can call your O(1) algorithm is O(n!) algorithm and be technically correct.
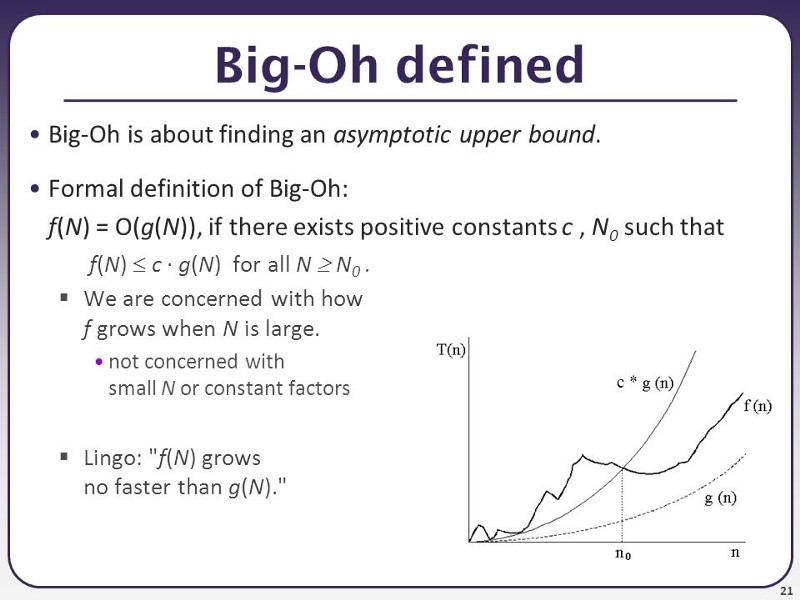
Here is a picture, that may help a little bit. The n is input size, and f(n) is how long does the algorithm runs (i.e how many instructions) it takes to calculate it for input for size n, i.e for finding smallest element in an array, n would be the number of elements in the array. g(n) is then the function you have in O, so if you have O(n^2) algorithm, the g(n) = n^2
Basically, you are looking for how quickly it grows for extreme values of N, while also disregarding constants. The graph representation probably isn’t too useful for figuring the O value, but it can help a little bit with understanding it - you want to find a O function where from one point onward (n0), the f(n) is under the O function all the way into infinity.
Also constant time is not always the fastest
plot twist to make it worse: you put in in an
onInputhook without even a debounceN00b. True pros accomplish O((n^2)!)
Your computer explodes at 4 elements
How the fuck?!
It may be efficient, not scalable for sure
Imagine if the algorithm were in Θ(n!²), that would be even worse
You mean omega, not theta
Did you write an algorithm to manually drag and drop elements?
For me, my common result would be something like O(shit).
Oh my god, that’s inefficient as hell.
It has been a while since I have to deal with problem complexities in college, is there even class of problems that would require something like this, or is there a proven upper limit/can this be simplified? I don’t think I’ve ever seen O(n!^k) class of problems.
Hmm, iirc non-deterministic turing machines should be able to solve most problems, but I’m not sure we ever talked about problems that are not NP. Are there such problems? And how is the problem class even called?
Oh, right, you also have EXP and NEXP. But that’s the highest class on wiki, and I can’t find if it’s proven that it’s enough for all problems. Is there a FACT and NFACT class?
Wait… How can time ever not be constant? Can we stop time?! 😮








